Cones of orthogonal Shimura subvarieties and equidistribution
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
Let X be an orthogonal Shimura variety, and let \(\mathcal {C}^{\textrm{ort}}_{r}(X)\) be the cone generated by the cohomology classes of orthogonal Shimura subvarieties in X of dimension r. We investigate the asymptotic properties of the generating rays of \(\mathcal {C}^{\textrm{ort}}_{r}(X)\) for large values of r. They accumulate towards rays generated by wedge products of the Kähler class of X and the fundamental class of an orthogonal Shimura subvariety. We also compare \(\mathcal {C}^{\textrm{ort}}_{r}(X)\) with the cone generated by the special cycles of dimension r. The main ingredient to achieve the results above is the equidistribution of orthogonal Shimura subvarieties.
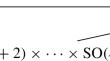
正交志村子变量的圆锥和等分布
让 X 是一个正交志村变,让 \(\mathcal {C}^{\textrm{ort}}_{r}}(X)\) 是维数为 r 的 X 中正交志村子变的同调类所生成的锥。我们研究了 r 大值时\(\mathcal {C}^{textrm{ort}}_{r}(X)\) 的生成射线的渐近性质,它们向由 X 的 Kähler 类和正交 Shimura 子变量的基类的楔积生成的射线累积。我们还将\(\mathcal {C}^{\textrm{ort}}_{r}(X)\) 与维数为 r 的特殊循环生成的圆锥进行了比较。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Manuscripta Mathematica
数学-数学
CiteScore
1.40
自引率
0.00%
发文量
86
审稿时长
6-12 weeks
期刊介绍:
manuscripta mathematica was founded in 1969 to provide a forum for the rapid communication of advances in mathematical research. Edited by an international board whose members represent a wide spectrum of research interests, manuscripta mathematica is now recognized as a leading source of information on the latest mathematical results.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


