Reduced polygons in the hyperbolic plane
IF 0.5
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
For a hyperplane H supporting a convex body C in the hyperbolic space \(\mathbb {H}^d\), we define the width of C determined by H as the distance between H and a most distant ultraparallel hyperplane supporting C. The minimum width of C over all supporting H is called the thickness \(\Delta (C)\) of C. A convex body \(R \subset \mathbb {H}^{d}\) is said to be reduced if \(\Delta (Z) < \Delta (R)\) for every convex body Z properly contained in R. We describe a class of reduced polygons in \(\mathbb {H}^{2}\) and present some properties of them. In particular, we estimate their diameters in terms of their thicknesses.
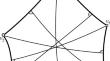
双曲面中的还原多边形
对于双曲空间 \(\mathbb {H}^{d}\)中支持凸体 C 的超平面 H,我们将 H 确定的 C 的宽度定义为 H 与支持 C 的最远超平行超平面之间的距离。我们描述了一类在 \(\mathbb {H}^{2}\) 中的还原多边形,并提出了它们的一些性质。特别是,我们用它们的厚度来估计它们的直径。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Archiv der Mathematik
数学-数学
CiteScore
1.10
自引率
0.00%
发文量
117
审稿时长
4-8 weeks
期刊介绍:
Archiv der Mathematik (AdM) publishes short high quality research papers in every area of mathematics which are not overly technical in nature and addressed to a broad readership.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


