Elliptic Analogue of the Vershik–Kerov Limit Shape
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
We review the limit shape problem for the Plancherel measure and its generalizations found in supersymmetric gauge theory instanton count. We focus on the measure, interpolating between the Plancherel measure and the uniform measure, a \(U(1)\) case of \(\mathcal{N}=2^{*}\) gauge theory. We give the formula for its limit shape in terms of elliptic functions, generalizing the trigonometric “arcsin” law of Vershik–Kerov and Logan–Schepp.
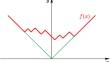
Vershik-Kerov 极限形状的椭圆类似物
摘要 我们回顾了普朗切尔量度的极限形状问题及其在超对称规理论瞬子计数中的泛化。我们关注的是介于普朗切尔量度和均匀量度之间的量度,它是\(\mathcal{N}=2^{*}\)规理论的一种(U(1)\)情况。我们用椭圆函数给出了它的极限形状公式,概括了 Vershik-Kerov 和 Logan-Schepp 的三角函数 "arcsin "定律。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
0.90
自引率
0.00%
发文量
7
审稿时长
>12 weeks
期刊介绍:
Functional Analysis and Its Applications publishes current problems of functional analysis, including representation theory, theory of abstract and functional spaces, theory of operators, spectral theory, theory of operator equations, and the theory of normed rings. The journal also covers the most important applications of functional analysis in mathematics, mechanics, and theoretical physics.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


