Upwind Bicompact Schemes for Hyperbolic Conservation Laws

Abstract

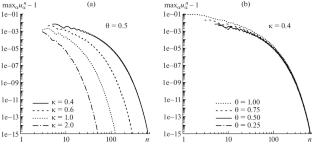
Upwind bicompact schemes of third-order approximation in space are presented for the first time. A formula is obtained for the transition factor of an arbitrary fully discrete bicompact scheme with Runge–Kutta time stepping. Stability and monotonicity of a scheme of first order in time are investigated, and the dissipative and dispersion properties of a scheme of third order in time are analyzed. Advantages of the new schemes over their centered counterparts are demonstrated.