Unsupervised learning of topological non-Abelian braiding in non-Hermitian bands

Abstract

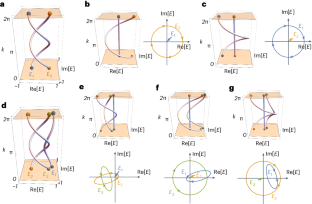
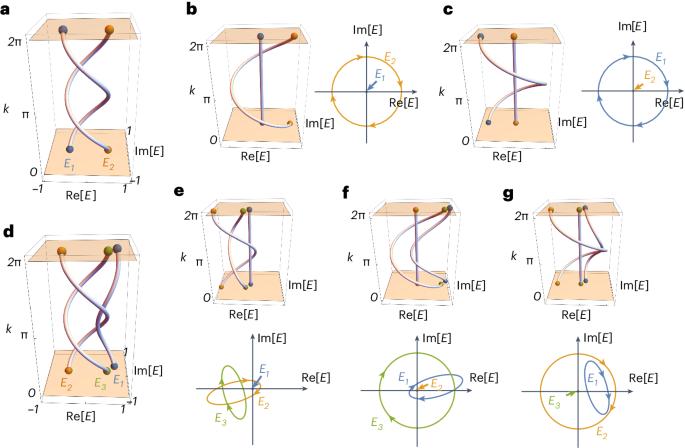
The topological classification of energy bands has laid the foundation for the discovery of various topological phases of matter in recent decades. While previous work focused on real-energy bands in Hermitian systems, recent studies have shifted attention to the intriguing topology of complex-energy, or non-Hermitian, bands, freeing them from the constraint of energy conservation. For example, the spectral winding of complex-energy bands can give rise to unique topological structures such as braids, holding substantial promise for advancing quantum computing. However, discussions of complex-energy braids have been predominantly limited to the Abelian braid group $${{\mathbb{B}}}_{2}$$ owing to its relative simplicity. Identifying topological non-Abelian braiding remains challenging, as it lacks a universally applicable topological invariant for characterization. Here we present a machine learning algorithm for the unsupervised identification of non-Abelian braiding within multiple complex-energy bands. We demonstrate that the results are consistent with Artin’s well-known topological equivalence conditions in braiding. Inspired by these findings, we introduce a winding matrix as a topological invariant for characterizing braiding topology. The winding matrix also reveals the bulk-edge correspondence of non-Hermitian bands with non-Abelian braiding. Finally, we extend our approach to identify non-Abelian braiding topology in two-dimensional and three-dimensional exceptional semimetals and address the unknotting problem in an unsupervised manner. The topological classification of complex-energy bands has uncovered various topological phases beyond Hermitian systems. Long and colleagues exploit unsupervised learning to fully identify the non-Abelian braiding topology of non-Hermitian bands.