On Vertices of Frontals in the Euclidean Plane
Bulletin of the Brazilian Mathematical Society, New Series
Pub Date : 2024-07-04
DOI:10.1007/s00574-024-00410-x
引用次数: 0
Abstract
We investigate vertices for plane curves with singular points. As plane curves with singular points, we consider Legendre curves (respectively, Legendre immersions) in the unit tangent bundle over the Euclidean plane and frontals (respectively, fronts) in the Euclidean plane. We define a vertex using evolutes of frontals. After that we define a vertex of a frontal in the general case. It is also known that the four vertex theorem does not hold for simple closed fronts. We give conditions under which a frontal has a vertex and the four vertex theorem holds for closed frontals. We also give examples and counter examples of the four vertex theorem.
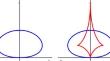
论欧几里得平面中的正面顶点
我们研究具有奇异点的平面曲线的顶点。作为有奇异点的平面曲线,我们考虑了欧几里得平面上单位切线束中的 Legendre 曲线(分别为 Legendre 沉浸)和欧几里得平面上的 frontals(分别为 frontts)。我们用正面的演化来定义顶点。然后,我们定义一般情况下的锋顶点。我们还知道,四顶点定理对于简单的封闭前沿并不成立。我们给出了正面有顶点和四顶点定理对封闭正面成立的条件。我们还给出了四顶点定理的实例和反例。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


