Stability via closure relations with applications to dissipative and port-Hamiltonian systems
IF 1.2
3区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
We consider differential operators A that can be represented by means of a so-called closure relation in terms of a simpler operator \(A_{{\text {ext}}}\) defined on a larger space. We analyse how the spectral properties of A and \(A_{{\text {ext}}}\) are related and give sufficient conditions for exponential stability of the semigroup generated by A in terms of the semigroup generated by \(A_{{\text {ext}}}\). As applications we study the long-term behaviour of a coupled wave–heat system on an interval, parabolic equations on bounded domains that are coupled by matrix-valued potentials, and of linear infinite-dimensional port-Hamiltonian systems with dissipation on an interval.
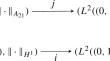
通过闭合关系实现稳定性,并应用于耗散系统和端口-哈密尔顿系统
我们考虑的微分算子 A 可以通过所谓的闭合关系用定义在更大空间上的更简单算子 \(A_{{\text {ext}}\) 来表示。我们分析了 A 和 \(A_{\text {ext}}\)的谱性质是如何相关的,并给出了由 A 产生的半群在由\(A_{\text {ext}}\)产生的半群方面指数稳定性的充分条件。作为应用,我们研究了区间上耦合波热系统的长期行为、有界域上由矩阵值势能耦合的抛物方程以及区间上具有耗散的线性无穷维端口-哈密顿系统。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
2.30
自引率
7.10%
发文量
90
审稿时长
>12 weeks
期刊介绍:
The Journal of Evolution Equations (JEE) publishes high-quality, peer-reviewed papers on equations dealing with time dependent systems and ranging from abstract theory to concrete applications.
Research articles should contain new and important results. Survey articles on recent developments are also considered as important contributions to the field.
Particular topics covered by the journal are:
Linear and Nonlinear Semigroups
Parabolic and Hyperbolic Partial Differential Equations
Reaction Diffusion Equations
Deterministic and Stochastic Control Systems
Transport and Population Equations
Volterra Equations
Delay Equations
Stochastic Processes and Dirichlet Forms
Maximal Regularity and Functional Calculi
Asymptotics and Qualitative Theory of Linear and Nonlinear Evolution Equations
Evolution Equations in Mathematical Physics
Elliptic Operators

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


