Slip-discreteness-corrected strain gradient crystal plasticity (SDC-SGCP) theory
Abstract
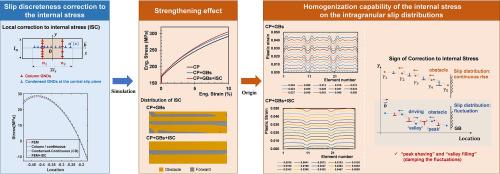
Strain gradient plasticity theory addresses the plastic strain gradient induced hardening by considering the internal stress and Taylor hardening associated with the geometrically necessary dislocations (GNDs). However, the continuum description of internal stress associated with GNDs is inaccurate due to the coarsening of discrete dislocations. Corrections are thus derived as the difference between the stresses produced by the continuous configuration and the discrete configuration. We further demonstrate the capability of this correction in effectively capturing the internal stress induced strengthening effect associated with GNDs, and elucidate that its role in strengthening is to homogenize the deformation and extend the influence of grain boundaries into the interior of grains within polycrystals. This capability to capture intragranular slip distribution is validated through the simulation of a polycrystalline tensile experiment. This work explains the limitations of classical crystal plasticity theory under high strain gradients and offers a straightforward yet robust slip discreteness correction to crystal plasticity with transparent input from dislocation theory, opening a new perspective for the connections between continuum crystal plasticity theory and dislocation theory.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


