Multiplicity and Concentration Behavior of Solutions to a Class of Fractional Kirchhoff Equation Involving Exponential Nonlinearity
引用次数: 0
Abstract
This article deals with the following fractional \(\frac{N}{s}\)-Laplace Kichhoff equation involving exponential growth of the form:
$$\begin{aligned} \varepsilon ^{N}K\left( [u]_{s,\frac{N}{s}}^{\frac{N}{s}}\right) (-\Delta )_{{N}/{s}}^{s}u+Z(x)|u|^{\frac{N}{s}-2}u=f(u)\;\text {in}\; \mathbb R^{N}, \end{aligned}$$where \(\varepsilon >0\) is a parameter, \(s\in (0,1)\) and \((-\Delta )_p^s\) is the fractional p-Laplace operator with \(p=\frac{N}{s}\ge 2\), K is a Kirchhoff function, f is a continuous function with exponential growth and Z is a potential function possessing a local minimum. Under some suitable conditions, we obtain the existence, multiplicity and concentration of solutions to the above problem via penalization methods and Lyusternik-Schnirelmann theory.
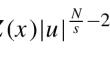
涉及指数非线性的一类分数基尔霍夫方程解的多重性和集中行为
本文讨论以下涉及指数增长形式的分数(\frac{N}{s}\)-拉普拉斯-基霍夫方程: $$\begin{aligned}\varepsilon ^{N}K\left( [u]_{s,\frac{N}{s}}^{\frac{N}{s}} 右) (-\Delta )_{{N}/{s}}^{s}u+Z(x)|u|^{frac{N}{s}-2}u=f(u)\;\text {in}\;\mathbb R^{N}, \end{aligned}$$其中 \(\varepsilon >;0)是一个参数,(s/in (0,1))和((-\Delta )_p^s\) 是分数p-拉普拉斯算子,其中(p=\frac{N}{s}\ge 2\),K是一个基尔霍夫函数,f是一个指数增长的连续函数,Z是一个具有局部最小值的势函数。在一些合适的条件下,我们通过惩罚方法和 Lyusternik-Schnirelmann 理论得到了上述问题解的存在性、多重性和集中性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


