Using the vector of the ideality of correlation to simulate the zeta potential of nanoparticles under different experimental conditions, represented by quasi-SMILES
Abstract
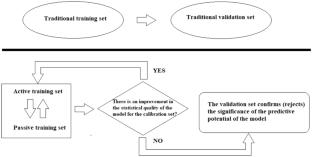
The modified version of quasi-SMILES is studied. Unlike the previous ones, the new version allows building codes of experimental conditions in a user-friendly (easily interpreted) form. The quasi-SMILES can be a convenient basis for discussion between experimentalists and developers of models. The optimal descriptors for regression one-parameter models were calculated with the Monte Carlo method, using the vector of ideality of correlation. The vector of the ideality of correlation has two components: (i) the index of ideality of correlation (IIC) and (ii) the correlation intensity index (CII). Both the indices are components of the stochastic Monte Carlo process. The contribution of these indices is paradoxical: they improve the statistical quality of a model on the external validation set but to the detriment of the statistical quality of the model for the training set. Taking into account IIC and CII values for the Monte Carlo optimization gives an improvement of models of zeta potential of considered nanoparticles. The described approach is convenient for modelling the zeta potential of the considered nanoparticles. No less important is the universality of the use of quasi-SMILES as a means for studying the values of endpoints in the form of mathematical functions of not only the structures of the simulated objects (nanoparticles) but also the experimental conditions.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


