Promising directions of machine learning for partial differential equations
IF 12
Q1 COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS
引用次数: 0
Abstract
Partial differential equations (PDEs) are among the most universal and parsimonious descriptions of natural physical laws, capturing a rich variety of phenomenology and multiscale physics in a compact and symbolic representation. Here, we examine several promising avenues of PDE research that are being advanced by machine learning, including (1) discovering new governing PDEs and coarse-grained approximations for complex natural and engineered systems, (2) learning effective coordinate systems and reduced-order models to make PDEs more amenable to analysis, and (3) representing solution operators and improving traditional numerical algorithms. In each of these fields, we summarize key advances, ongoing challenges, and opportunities for further development. Machine learning has enabled major advances in the field of partial differential equations. This Review discusses some of these efforts and other ongoing challenges and opportunities for development.
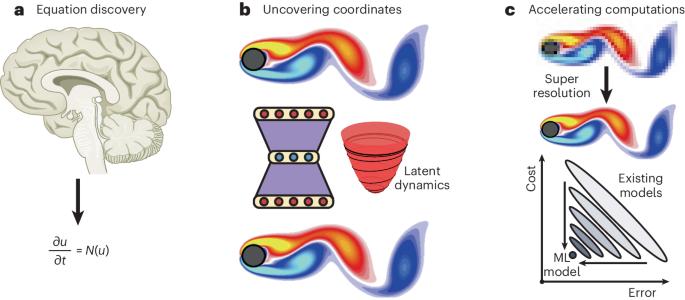
偏微分方程机器学习的发展方向。
偏微分方程(PDEs)是对自然物理规律最通用、最简洁的描述之一,它以紧凑的符号表示捕捉了丰富多样的现象学和多尺度物理学。在此,我们将探讨机器学习正在推动的几种有前途的多导方程研究途径,包括:(1) 为复杂的自然和工程系统发现新的支配多导方程和粗粒度近似值;(2) 学习有效坐标系和降阶模型,使多导方程更易于分析;(3) 表示求解算子并改进传统的数值算法。在上述每个领域,我们都总结了主要进展、当前挑战和进一步发展的机遇。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


