Range-limited Heaps’ law for functional DNA words in the human genome

Abstract

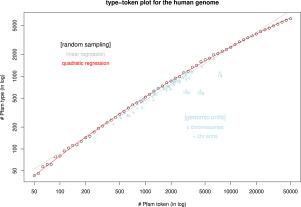
Heaps’ or Herdan-Heaps’ law is a linguistic law describing the relationship between the vocabulary/dictionary size (type) and word counts (token) to be a power-law function. Its existence in genomes with certain definition of DNA words is unclear partly because the dictionary size in genome could be much smaller than that in a human language. We define a DNA word as a coding region in a genome that codes for a protein domain. Using human chromosomes and chromosome arms as individual samples, we establish the existence of Heaps’ law in the human genome within limited range. Our definition of words in a genomic or proteomic context is different from other definitions such as over-represented k-mers which are much shorter in length. Although an approximate power-law distribution of protein domain sizes due to gene duplication and the related Zipf’s law is well known, their translation to the Heaps’ law in DNA words is not automatic. Several other animal genomes are shown herein also to exhibit range-limited Heaps’ law with our definition of DNA words, though with various exponents. When tokens were randomly sampled and sample sizes reach to the maximum level, a deviation from the Heaps’ law was observed, but a quadratic regression in log–log type-token plot fits the data perfectly. Investigation of type-token plot and its regression coefficients could provide an alternative narrative of reusage and redundancy of protein domains as well as creation of new protein domains from a linguistic perspective.