Computing the committor with the committor to study the transition state ensemble
IF 12
Q1 COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS
引用次数: 0
Abstract
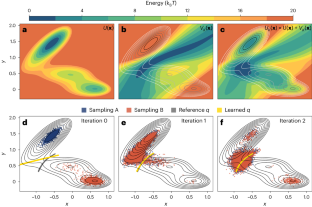
The study of the kinetic bottlenecks that hinder the rare transitions between long-lived metastable states is a major challenge in atomistic simulations. Here we propose a method to explore the transition state ensemble, which is the distribution of configurations that the system passes through as it translocates from one metastable basin to another. We base our method on the committor function and the variational principle that it obeys. We find its minimum through a self-consistent procedure that starts from information limited to the initial and final states. Right from the start, our procedure allows the sampling of very many transition state configurations. With the help of the variational principle, we perform a detailed analysis of the transition state ensemble, ranking quantitatively the degrees of freedom mostly involved in the transition and enabling a systematic approach for the interpretation of simulation results and the construction of efficient physics-informed collective variables. A self-consistent iterative procedure is proposed to compute the committor function for rare events, via a variational principle, and extensively sample the transition state ensemble, allowing for the identification of the relevant variables in the process.

计算承诺器与承诺器,研究过渡态集合
研究阻碍长寿命态之间罕见转变的动力学瓶颈是原子模拟的一大挑战。在这里,我们提出了一种探索过渡态集合的方法,过渡态集合是系统从一个态转移到另一个态时所经过的构型分布。我们的方法基于委托函数及其遵循的变分原理。我们从仅限于初始和最终状态的信息出发,通过自洽程序找到其最小值。从一开始,我们的程序就允许对非常多的过渡状态配置进行采样。在变分原理的帮助下,我们对过渡态集合进行了详细分析,定量排序了过渡过程中主要涉及的自由度,并为解释模拟结果和构建高效的物理集合变量提供了系统方法。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


