A Characterization of Graphs with Semitotal Domination Number One-Third Their Order
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
In an isolate-free graph G, a subset S of vertices is a semitotal dominating set of G if it is a dominating set of G and every vertex in S is within distance 2 of another vertex of S. The semitotal domination number of G, denoted by \(\gamma _{t2}(G)\), is the minimum cardinality of a semitotal dominating set in G. Zhu et al. (Gr Combin 33, 1119–1130, 2017) proved that if \(G\notin \{K_4,N_2\}\) is a connected claw-free cubic graph of order n, then \(\gamma _{t2}(G)\le \frac{n}{3}\), which is sharp. They proposed the problem of characterizing the extremal graphs. We completely solve this problem. There are ten classes of graphs, three of which are infinite families of graphs.
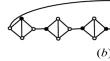
具有三分之一阶半总支配数的图的特征
在无孤立图 G 中,如果顶点子集 S 是 G 的支配集,且 S 中的每个顶点与 S 中另一个顶点的距离都在 2 以内,则该顶点子集 S 是 G 的半总支配集。G 的半总支配数用 \(\gamma _{t2}(G)\) 表示,它是 G 中半总支配集的最小卡片度。Zhu 等人(Gr Combin 33, 1119-1130, 2017)证明了如果 \(G\notin \{K_4,N_2\}\) 是阶数为 n 的连通无爪立方图,那么 \(\gamma _{t2}(G)\le \frac{n}{3}\) 是尖锐的。他们提出了极值图的特征问题。我们完全解决了这个问题。有十类图,其中三类是无限图族。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Graphs and Combinatorics
数学-数学
CiteScore
1.00
自引率
14.30%
发文量
160
审稿时长
6 months
期刊介绍:
Graphs and Combinatorics is an international journal devoted to research concerning all aspects of combinatorial mathematics. In addition to original research papers, the journal also features survey articles from authors invited by the editorial board.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


