Modified projection method and strong convergence theorem for solving variational inequality problems with non-Lipschitz operators

IF 16.4 1区化学 Q1 CHEMISTRY, MULTIDISCIPLINARY

Accounts of Chemical Research Pub Date : 2024-06-01 DOI:10.1007/s11075-024-01851-7

Zhongbing Xie, Huanqin Wu, Liya Liu

引用次数: 0

Abstract

In this paper, we introduce a modified projection method and give a strong convergence theorem for solving variational inequality problems in real Hilbert spaces. Under mild assumptions, there exists a novel line-search rule that makes the proposed algorithm suitable for non-Lipschitz continuous and pseudo-monotone operators. Compared with other known algorithms in numerical experiments, it is shown that our algorithm has better numerical performance.

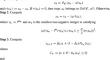
Abstract Image

查看原文本刊更多论文

解决非 Lipschitz 算子的变分不等式问题的修正投影法和强收敛定理

本文介绍了一种改进的投影法，并给出了求解实希尔伯特空间中变不等式问题的强收敛定理。在温和的假设条件下，存在一种新颖的线性搜索规则，使得所提出的算法适用于非 Lipschitz 连续和伪单调算子。数值实验表明，与其他已知算法相比，我们的算法具有更好的数值性能。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Accounts of Chemical Research 化学-化学综合

CiteScore

31.40

自引率

1.10%

发文量

312

审稿时长

2 months

期刊介绍： Accounts of Chemical Research presents short, concise and critical articles offering easy-to-read overviews of basic research and applications in all areas of chemistry and biochemistry. These short reviews focus on research from the author’s own laboratory and are designed to teach the reader about a research project. In addition, Accounts of Chemical Research publishes commentaries that give an informed opinion on a current research problem. Special Issues online are devoted to a single topic of unusual activity and significance. Accounts of Chemical Research replaces the traditional article abstract with an article "Conspectus." These entries synopsize the research affording the reader a closer look at the content and significance of an article. Through this provision of a more detailed description of the article contents, the Conspectus enhances the article's discoverability by search engines and the exposure for the research.