Extremal Graphs for the $$K_{1,2}$$ -Isolation Number of Graphs
IF 1.2
3区 数学
Q1 MATHEMATICS
Bulletin of the Malaysian Mathematical Sciences Society
Pub Date : 2024-05-28
DOI:10.1007/s40840-024-01711-6
引用次数: 0
Abstract
For any non-negative integer k and any graph G, a subset \(S\subseteq V(G)\) is said to be a \(K_{1,k+1}\)-isolating set of G if \(G-N[S]\) does not contain \(K_{1,k+1}\) as a subgraph. The \(K_{1,k+1}\)-isolation number of G, denoted by \(\iota _k(G)\), is the minimum cardinality of a \(K_{1,k+1}\)-isolating set of G. Recently, Zhang and Wu (2021) proved that if G is a connected n-vertex graph and \(G\notin \{P_3,C_3,C_6\}\), then \(\iota _1(G)\le \frac{2}{7}n\). In this paper, we characterize all extremal graphs attaining this bound, which resolves a problem proposed by Zhang and Wu (Discrete Appl Math 304:365–374, 2021).
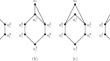
$$K_{1,2}$ -隔离数的极值图
对于任意非负整数k和任意图G,如果\(G-N[S]\)不包含作为子图的\(K_{1,k+1}\),那么子集\(S\subseteq V(G)\)被称为G的\(K_{1,k+1}\)隔离集。G 的隔离数用 \(\iota _k(G)\)表示,它是\(K_{1,k+1}\)-隔离集的最小卡片度。最近,Zhang 和 Wu(2021)证明了如果 G 是一个 n 个顶点的连通图,并且 \(G notin \{P_3,C_3,C_6}\), 那么 \(\iota _1(G)\le \frac{2}{7}n\).本文描述了所有达到此约束的极值图,解决了张和吴提出的问题(Discrete Appl Math 304:365-374, 2021)。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
2.40
自引率
8.30%
发文量
176
审稿时长
3 months
期刊介绍:
This journal publishes original research articles and expository survey articles in all branches of mathematics. Recent issues have included articles on such topics as Spectral synthesis for the operator space projective tensor product of C*-algebras; Topological structures on LA-semigroups; Implicit iteration methods for variational inequalities in Banach spaces; and The Quarter-Sweep Geometric Mean method for solving second kind linear fredholm integral equations.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


