Drift approximation by the modified Boris algorithm of charged-particle dynamics in toroidal geometry

IF 2.1 2区数学 Q1 MATHEMATICS, APPLIED

Numerische Mathematik Pub Date : 2024-05-24 DOI:10.1007/s00211-024-01416-9

Yanyan Shi

引用次数: 0

Abstract

In this paper, we study the dynamics of charged particles under a strong magnetic field in toroidal axi-symmetric geometry. Using modulated Fourier expansions of the exact and numerical solutions, the long-term drift motion of the exact solution in toroidal geometry is derived, and the error analysis of the large-stepsize modified Boris algorithm over long time is provided. Numerical experiments are conducted to illustrate the theoretical results.

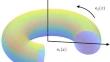
Abstract Image

查看原文本刊更多论文

环状几何中带电粒子动力学的改进鲍里斯算法漂移近似

本文研究了带电粒子在环形轴对称几何体强磁场下的动力学。利用精确解和数值解的调制傅里叶展开，推导了精确解在环形几何中的长期漂移运动，并提供了大步幅修正 Boris 算法在长时间内的误差分析。为说明理论结果，还进行了数值实验。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Numerische Mathematik 数学-应用数学

CiteScore

4.10

自引率

4.80%

发文量

审稿时长

6-12 weeks

期刊介绍： Numerische Mathematik publishes papers of the very highest quality presenting significantly new and important developments in all areas of Numerical Analysis. "Numerical Analysis" is here understood in its most general sense, as that part of Mathematics that covers: 1. The conception and mathematical analysis of efficient numerical schemes actually used on computers (the "core" of Numerical Analysis) 2. Optimization and Control Theory 3. Mathematical Modeling 4. The mathematical aspects of Scientific Computing