Isogeometric Shape Optimization of Reissner–Mindlin Shell with Analytical Sensitivity and Application to Cellular Sandwich Structures
Abstract
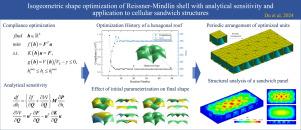
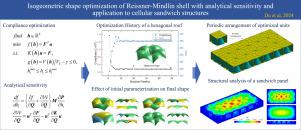
Structural shape optimization plays a significant role in structural design, as it can find an appropriate layout and shape to improve structural performance. Isogeometric analysis provides a promising framework for structural shape optimization, unifying the design model and analysis model in the optimization process. This paper presents an adjoint-based analytical sensitivity for isogeometric shape optimization of Reissner–Mindlin shell structures. The shell structures are modeled by multiple NURBS surfaces and design variables are associated with the position of control points. A multilevel approach is performed with a coarse mesh for the design model and a dense mesh for the analysis model. The sensitivity propagation is achieved through a transformation matrix between the design and analysis models. Structural compliance minimization problems with and without constraints are studied and the optimization history shows that the optimization can converge quickly within fewer iterations. The developed formulations are validated through several numerical examples and applied to the optimization of cellular sandwich structures, which are widely used in engineering applications. Numerical results show that optimized sandwich panels can achieve better performance in bending resistance.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


