Bayesian pairwise meta-analysis of time-to-event outcomes in the presence of non-proportional hazards: A simulation study of flexible parametric, piecewise exponential and fractional polynomial models

Abstract

Background

Traditionally, meta-analysis of time-to-event outcomes reports a single pooled hazard ratio assuming proportional hazards (PH). For health technology assessment evaluations, hazard ratios are frequently extrapolated across a lifetime horizon. However, when treatment effects vary over time, an assumption of PH is not always valid. The Royston-Parmar (RP), piecewise exponential (PE), and fractional polynomial (FP) models can accommodate non-PH and provide plausible extrapolations of survival curves beyond observed data.

Methods

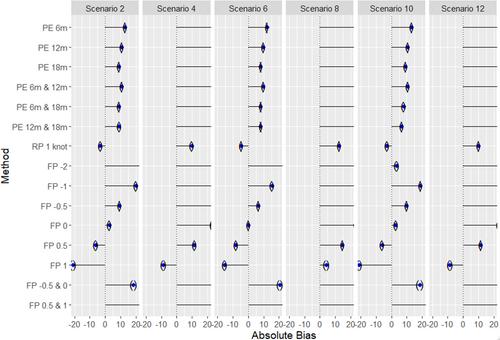
Simulation study to assess and compare the performance of RP, PE, and FP models in a Bayesian framework estimating restricted mean survival time difference (RMSTD) at 50 years from a pairwise meta-analysis with evidence of non-PH. Individual patient data were generated from a mixture Weibull distribution. Twelve scenarios were considered varying the amount of follow-up data, number of trials in a meta-analysis, non-PH interaction coefficient, and prior distributions. Performance was assessed through bias and mean squared error. Models were applied to a metastatic breast cancer example.

Results

FP models performed best when the non-PH interaction coefficient was 0.2. RP models performed best in scenarios with complete follow-up data. PE models performed well on average across all scenarios. In the metastatic breast cancer example, RMSTD at 50-years ranged from −14.6 to 8.48 months.

Conclusions

Synthesis of time-to-event outcomes and estimation of RMSTD in the presence of non-PH can be challenging and computationally intensive. Different approaches make different assumptions regarding extrapolation and sensitivity analyses varying key assumptions are essential to check the robustness of conclusions to different assumptions for the underlying survival function.