Borsik’s Properties of Topological Spaces and Their Applications
IF 1.2
3区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
Let X be an uncountable Polish space. L̆ubica Holá showed recently that there are \(2^{\mathfrak {c}}\) quasi-continuous real valued functions defined on the uncountable Polish space X that are not Borel measurable. Inspired by Holá’s result, we are extending it in two directions. First, we prove that if X is an uncountable Polish space and Y is any Hausdorff space with \(|Y|\ge 2\) then the family of all non-Borel measurable quasi-continuous functions has cardinality \(\ge 2^{{\mathfrak {c}}}\). Secondly, we show that the family of quasi-continuous non Borel functions from X to Y may contain big algebraic structures.
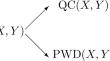
博尔西克拓扑空间特性及其应用
让 X 是一个不可数的波兰空间。L̆ubica Holá 最近证明,存在定义在不可数波兰空间 X 上的(2^{\mathfrak {c}})准连续实值函数,而这些函数不是 Borel 可测的。受霍拉结果的启发,我们在两个方向上对其进行了扩展。首先,我们证明如果 X 是一个不可数波兰空间,Y 是任何具有 \(|Y|\ge 2\) 的 Hausdorff 空间,那么所有非 Borel 可测的准连续函数的族具有 cardinality \(\ge 2^{\{mathfrak {c}}\) 。)其次,我们证明了从 X 到 Y 的非 Borel 准连续函数族可能包含大代数结构。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Results in Mathematics
数学-数学
CiteScore
1.90
自引率
4.50%
发文量
198
审稿时长
6-12 weeks
期刊介绍:
Results in Mathematics (RM) publishes mainly research papers in all fields of pure and applied mathematics. In addition, it publishes summaries of any mathematical field and surveys of any mathematical subject provided they are designed to advance some recent mathematical development.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


