Critical Subgraphs of Schrijver Graphs for the Fractional Chromatic Number

Abstract

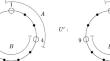
Schrijver graphs are vertex-color-critical subgraphs of Kneser graphs having the same chromatic number. They also share the value of their fractional chromatic number but Schrijver graphs are not critical for that. Here we present an induced subgraph of every Schrijver graph that is vertex-critical with respect to the fractional chromatic number. These subgraphs turn out to be isomorphic with certain circular complete graphs. We also characterize the critical edges within this subgraph.