Gap for geometric canonical height functions
IF 1
3区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
We prove the existence of a gap around zero for canonical height functions associated with endomorphisms of projective spaces defined over complex function fields. We also prove that if the rational points of height zero are Zariski dense, then the endomorphism is birationally isotrivial. As a corollary, by a result of S. Cantat and J. Xie, we have a geometric Northcott property on projective plane in the same spirit of results of R. Benedetto, M. Baker and L. Demarco on the projective line.
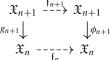
几何标准高度函数的差距
我们证明了与定义在复变函数域上的投影空间内定形相关的典范高度函数存在零附近的缺口。我们还证明,如果高度为零的有理点是扎里斯基密集的,那么内态性就是双等价的。作为推论,通过 S. Cantat 和 J. Xie 的一个结果,我们在投影平面上得到了几何诺斯考特属性,其精神与 R. Benedetto、M. Baker 和 L. Demarco 在投影线上的结果相同。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.60
自引率
0.00%
发文量
236
审稿时长
3-6 weeks
期刊介绍:
"Mathematische Zeitschrift" is devoted to pure and applied mathematics. Reviews, problems etc. will not be published.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


