On the Maximal Distance Between the Centers of Mass of a Planar Convex Body and Its Boundary

IF 0.6 3区数学 Q4 COMPUTER SCIENCE, THEORY & METHODS

Discrete & Computational Geometry Pub Date : 2024-05-06 DOI:10.1007/s00454-024-00650-0

Fedor Nazarov, Dmitry Ryabogin, Vladyslav Yaskin

引用次数: 0

Abstract

We prove that the length of the projection of the vector joining the centers of mass of a convex body on the plane and of its boundary to an arbitrary direction does not exceed \(\frac{1}{6}\) of the body width in this direction. It follows that the distance between these centers of mass does not exceed \(\frac{1}{6}\) of the diameter of the body and \(\frac{1}{12}\) of its boundary length. None of those constants can be improved.

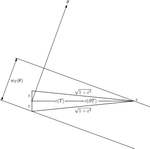
Abstract Image

查看原文本刊更多论文

论平面凸体质量中心与其边界之间的最大距离

我们证明，连接平面上凸体质量中心及其边界的矢量在任意方向上的投影长度不超过该方向上体宽的\(\frac{1}{6}\)。由此可见，这些质心之间的距离不会超过凸体直径的 \(\frac{1}{6}\) 和边界长度的 \(\frac{1}{12}\) 。这些常数都无法改进。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Discrete & Computational Geometry 数学-计算机：理论方法

CiteScore

1.80

自引率

12.50%

发文量

审稿时长

6-12 weeks

期刊介绍： Discrete & Computational Geometry (DCG) is an international journal of mathematics and computer science, covering a broad range of topics in which geometry plays a fundamental role. It publishes papers on such topics as configurations and arrangements, spatial subdivision, packing, covering, and tiling, geometric complexity, polytopes, point location, geometric probability, geometric range searching, combinatorial and computational topology, probabilistic techniques in computational geometry, geometric graphs, geometry of numbers, and motion planning.