Optimal Analysis of Method with Batching for Monotone Stochastic Finite-Sum Variational Inequalities

IF 0.5 4区数学 Q3 MATHEMATICS

Doklady Mathematics Pub Date : 2024-03-25 DOI:10.1134/s1064562423701582

A. Pichugin, M. Pechin, A. Beznosikov, A. Savchenko, A. Gasnikov

引用次数: 0

Abstract

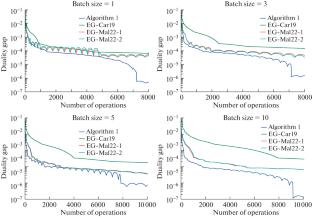
Variational inequalities are a universal optimization paradigm that is interesting in itself, but also incorporates classical minimization and saddle point problems. Modern realities encourage to consider stochastic formulations of optimization problems. In this paper, we present an analysis of a method that gives optimal convergence estimates for monotone stochastic finite-sum variational inequalities. In contrast to the previous works, our method supports batching and does not lose the oracle complexity optimality. The effectiveness of the algorithm, especially in the case of small but not single batches is confirmed experimentally.

Abstract Image

查看原文本刊更多论文

单调随机有限和变分不等式的批处理方法优化分析

摘要变量不等式是一种通用的优化范式，它本身就很有趣，而且还包含经典的最小化和鞍点问题。现代社会鼓励考虑优化问题的随机形式。本文分析了一种方法，它能给出单调随机有限和变分不等式的最佳收敛估计值。与前人的研究相比，我们的方法支持批处理，而且不会失去甲骨文复杂性的最优性。实验证实了该算法的有效性，尤其是在批量较小但不单一的情况下。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Doklady Mathematics 数学-数学

CiteScore

1.00

自引率

16.70%

发文量

审稿时长

3-6 weeks

期刊介绍： Doklady Mathematics is a journal of the Presidium of the Russian Academy of Sciences. It contains English translations of papers published in Doklady Akademii Nauk (Proceedings of the Russian Academy of Sciences), which was founded in 1933 and is published 36 times a year. Doklady Mathematics includes the materials from the following areas: mathematics, mathematical physics, computer science, control theory, and computers. It publishes brief scientific reports on previously unpublished significant new research in mathematics and its applications. The main contributors to the journal are Members of the RAS, Corresponding Members of the RAS, and scientists from the former Soviet Union and other foreign countries. Among the contributors are the outstanding Russian mathematicians.