The Threshold of a Stochastic SIRS Epidemic Model with a General Incidence

Abstract

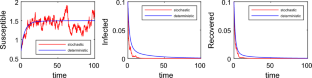
In this article, a SIRS epidemic model with a general incidence rate is proposed and investigated. We briefly verify the global existence of a unique positive solution for the proposed system. Moreover, and unlike other works, we were able to find the stochastic threshold \(\mathcal {R}_s\) of the proposed model which was used for the discussion of the persistence in mean and extinction of the disease. Moreover, we utilize stochastic Lyapunov functions to show under sufficient conditions the existence and uniqueness of stationary distributions of the solution. Lastly, numerical simulation is executed to conform our analytical results.