Local scattering matrix for a degenerate avoided-crossing in the non-coupled regime
IF 1.3
3区 物理与天体物理
Q3 PHYSICS, MATHEMATICAL
引用次数: 0
Abstract
A Landau–Zener-type formula for a degenerate avoided-crossing is studied in the non-coupled regime. More precisely, a \(2\times 2\) system of first-order h-differential operator with \(\mathcal {O}(\varepsilon )\) off-diagonal part is considered in 1D. Asymptotic behavior as \(\varepsilon h^{m/(m+1)}\rightarrow 0^+\) of the local scattering matrix near an avoided-crossing is given, where m stands for the contact order of two curves of the characteristic set. A generalization including the cases with vanishing off-diagonals and non-Hermitian symbols is also given.
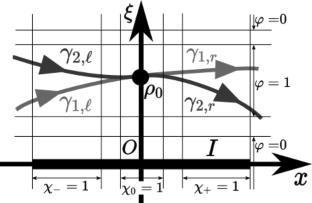
非耦合系统中退化避免交叉的局部散射矩阵
在非耦合机制中,研究了退化避免交叉的兰道-齐纳型公式。更确切地说,在一维中考虑了一个一阶 h 微分算子的 (2 次 2)系统,其对角线部分为 (\(\mathcal {O}(\varepsilon )\) off-diagonal 部分。给出了避免交叉附近局部散射矩阵的渐近行为((\varepsilon h^{m/(m+1)}\rightarrow 0^+\),其中 m 代表特征集两条曲线的接触阶数。此外,还给出了包括对角线消失和非ermitian 符号情况的概括。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Letters in Mathematical Physics
物理-物理:数学物理
CiteScore
2.40
自引率
8.30%
发文量
111
审稿时长
3 months
期刊介绍:
The aim of Letters in Mathematical Physics is to attract the community''s attention on important and original developments in the area of mathematical physics and contemporary theoretical physics. The journal publishes letters and longer research articles, occasionally also articles containing topical reviews. We are committed to both fast publication and careful refereeing. In addition, the journal offers important contributions to modern mathematics in fields which have a potential physical application, and important developments in theoretical physics which have potential mathematical impact.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


