Triangle Percolation on the Grid
IF 0.6
3区 数学
Q4 COMPUTER SCIENCE, THEORY & METHODS
引用次数: 0
Abstract
We consider a geometric percolation process partially motivated by recent work of Hejda and Kala. Specifically, we start with an initial set \(X \subseteq {\mathbb {Z}}^2\), and then iteratively check whether there exists a triangle \(T \subseteq {\mathbb {R}}^2\) with its vertices in \({\mathbb {Z}}^2\) such that T contains exactly four points of \({\mathbb {Z}}^2\) and exactly three points of X. In this case, we add the missing lattice point of T to X, and we repeat until no such triangle exists. We study the limit sets S, the sets stable under this process, including determining their possible densities and some of their structure.
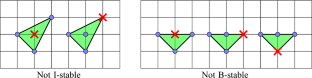
网格上的三角渗透
我们考虑了一个几何渗流过程,其部分动机来自 Hejda 和 Kala 的最新研究。具体来说,我们从一个初始集合(X)开始,然后迭代检查是否存在一个顶点在(X)中的三角形(T),使得 T 包含了(X)的四个点和三个点。在这种情况下,我们把 T 中缺失的网格点添加到 X 中,如此重复直到不存在这样的三角形为止。我们将研究极限集合 S,即在此过程中稳定的集合,包括确定它们可能的密度及其部分结构。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Discrete & Computational Geometry
数学-计算机:理论方法
CiteScore
1.80
自引率
12.50%
发文量
99
审稿时长
6-12 weeks
期刊介绍:
Discrete & Computational Geometry (DCG) is an international journal of mathematics and computer science, covering a broad range of topics in which geometry plays a fundamental role. It publishes papers on such topics as configurations and arrangements, spatial subdivision, packing, covering, and tiling, geometric complexity, polytopes, point location, geometric probability, geometric range searching, combinatorial and computational topology, probabilistic techniques in computational geometry, geometric graphs, geometry of numbers, and motion planning.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


