The focusing coupled modified Korteweg–de Vries equation with nonzero boundary conditions: the Riemann–Hilbert problem and soliton classification

IF 1 4区物理与天体物理 Q3 PHYSICS, MATHEMATICAL

Theoretical and Mathematical Physics Pub Date : 2024-04-26 DOI:10.1134/s004057792404007x

Xinxin Ma

引用次数: 0

Abstract

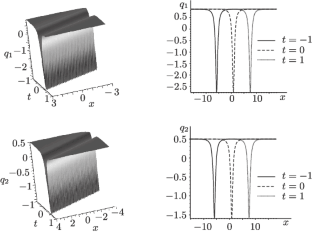
The focusing coupled modified Korteweg–de Vries equation with nonzero boundary conditions is investigated by the Riemann–Hilbert approach. Three symmetries are formulated to derive compact exact solutions. The solutions include six different types of soliton solutions and breathers, such as dark–dark, bright–bright, kink–dark–dark, kink–bright–bright solitons, and a breather–breather solution.

Abstract Image

查看原文本刊更多论文

具有非零边界条件的聚焦耦合修正科特韦格-德-弗里斯方程：黎曼-希尔伯特问题与孤子分类

摘要采用黎曼-希尔伯特方法研究了具有非零边界条件的聚焦耦合修正 Korteweg-de Vries 方程。通过三个对称性推导出紧凑的精确解。这些解包括六种不同类型的孤子解和呼吸器解，如暗-暗、亮-亮、磕-暗-暗、磕-亮-亮孤子，以及呼吸器-呼吸器解。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Theoretical and Mathematical Physics 物理-物理：数学物理

CiteScore

1.60

自引率

20.00%

发文量

103

审稿时长

4-8 weeks

期刊介绍： Theoretical and Mathematical Physics covers quantum field theory and theory of elementary particles, fundamental problems of nuclear physics, many-body problems and statistical physics, nonrelativistic quantum mechanics, and basic problems of gravitation theory. Articles report on current developments in theoretical physics as well as related mathematical problems. Theoretical and Mathematical Physics is published in collaboration with the Steklov Mathematical Institute of the Russian Academy of Sciences.