Inequalities involving the harmonic-arithmetic index
IF 0.9
Q2 MATHEMATICS
引用次数: 0
Abstract
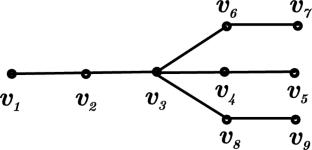
Let G be a simple graph with vertex set \(V=\{v_{1},v_{2},\ldots ,v_{n}\}\). The notion \(i\sim j\) is used to indicate that the vertices \(v_{i}\) and \(v_{j}\) of G are adjacent. For a vertex \(v_{i}\in V\), let \(d_{i}\) be the degree of \(v_{i}\). The harmonic-arithmetic (HA) index of G is defined as \(HA(G) =\sum _{i\sim j} 4d_id_j(d_i+d_j)^{-2}\). In this paper, a considerable number of inequalities involving the HA index and other topological indices are derived. For every obtained inequality, all the graphs that satisfy the equality case are also characterized.
涉及谐波算术指数的不等式
让 G 是一个简单图,其顶点集为(V={v_{1},v_{2},\ldots ,v_{n}\})。\(i\sim j\) 这个概念用来表示 G 的顶点 \(v_{i}\) 和 \(v_{j}\) 是相邻的。对于顶点 \(v_{i}\in V\), 让 \(d_{i}\) 是 \(v_{i}\) 的度数。G 的谐波算术(HA)指数定义为:\(HA(G) =\sum _{i\sim j} 4d_id_j(d_i+d_j)^{-2}\).本文推导了大量涉及 HA 指数和其他拓扑指数的不等式。对于每一个求得的不等式,所有满足相等情况的图形也都被表征出来。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


