NEW CONGRUENCES FOR THE TRUNCATED APPELL SERIES

Abstract

Liu [‘Supercongruences for truncated Appell series’, Colloq. Math. 158(2) (2019), 255–263] and Lin and Liu [‘Congruences for the truncated Appell series 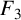$F_3$ and 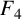$F_4$’, Integral Transforms Spec. Funct. 31(1) (2020), 10–17] confirmed four supercongruences for truncated Appell series. Motivated by their work, we give a new supercongruence for the truncated Appell series 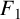$F_{1}$, together with two generalisations of this supercongruence, by establishing its q-analogues.