A note on the capacity estimate in metastability for generic configurations
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
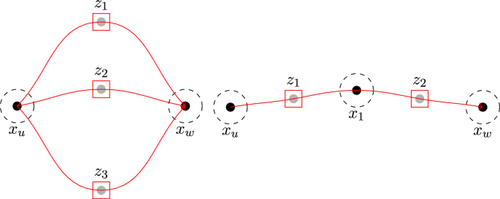
In this paper we further develop the ideas from Geometric Function Theory initially introduced in Avelin et al. (Commun Math Phys 404:401–437, 2023), to derive capacity estimate in metastability for arbitrary configurations. The novelty of this paper is twofold. First, the graph theoretical connection enables us to exactly compute the pre-factor in the capacity. Second, we complete the method from Avelin et al. (Commun Math Phys 404:401–437, 2023) by providing an upper bound using Geometric Function Theory together with Thompson’s principle, avoiding explicit constructions of test functions.
关于一般配置的代谢能力估计的说明
在本文中,我们进一步发展了最初在阿维林等人(Commun Math Phys 404:401-437, 2023)一文中提出的几何函数论的思想,推导出了任意配置的可转移性容量估计。本文的新颖之处有两方面。首先,图论联系使我们能够精确计算容量中的预因子。其次,我们利用几何函数理论和汤普森原理提供了一个上界,避免了测试函数的明确构造,从而完善了阿维林等人(Commun Math Phys 404:401-437, 2023)的方法。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Manuscripta Mathematica
数学-数学
CiteScore
1.40
自引率
0.00%
发文量
86
审稿时长
6-12 weeks
期刊介绍:
manuscripta mathematica was founded in 1969 to provide a forum for the rapid communication of advances in mathematical research. Edited by an international board whose members represent a wide spectrum of research interests, manuscripta mathematica is now recognized as a leading source of information on the latest mathematical results.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


