Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula
IF 0.9
3区 数学
Q1 MATHEMATICS
Proceedings of the Royal Society of Edinburgh Section A-Mathematics
Pub Date : 2024-04-16
DOI:10.1017/prm.2024.47
引用次数: 0
Abstract
Following the seminal paper by Bourgain, Brezis, and Mironescu, we focus on the asymptotic behaviour of some nonlocal functionals that, for each $u\in L^2(\mathbb {R}^N)$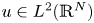 , are defined as the double integrals of weighted, squared difference quotients of $u$
, are defined as the double integrals of weighted, squared difference quotients of $u$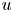 . Given a family of weights $\{\rho _{\varepsilon} \}$
. Given a family of weights $\{\rho _{\varepsilon} \}$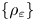 , $\varepsilon \in (0,\,1)$
, $\varepsilon \in (0,\,1)$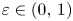 , we devise sufficient and necessary conditions on $\{\rho _{\varepsilon} \}$
, we devise sufficient and necessary conditions on $\{\rho _{\varepsilon} \}$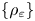 for the associated nonlocal functionals to converge as $\varepsilon \to 0$
for the associated nonlocal functionals to converge as $\varepsilon \to 0$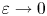 to a variant of the Dirichlet integral. Finally, some comparison between our result and the existing literature is provided.
to a variant of the Dirichlet integral. Finally, some comparison between our result and the existing literature is provided.
布尔干-布雷齐斯-米罗内斯库公式有效性的苛刻条件
继布尔甘(Bourgain)、布雷齐斯(Brezis)和米罗内斯库(Mironescu)的开创性论文之后,我们将重点放在一些非局部函数的渐近行为上,对于 L^2(\mathbb {R}^N)$ 中的每个 $u$,这些函数被定义为 $u$ 的加权平方差商的双积分。给定一个权值系列 $\{\rho _{\varepsilon}\$\varepsilon 在(0,\,1)$ 中,我们设计了关于 $\{rho _{\varepsilon} 的充分和必要条件。}\相关的非局部函数随着 $\varepsilon \to 0$ 收敛到迪里希特积分的变体上。最后,我们对我们的结果与现有文献进行了比较。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.00
自引率
0.00%
发文量
72
审稿时长
6-12 weeks
期刊介绍:
A flagship publication of The Royal Society of Edinburgh, Proceedings A is a prestigious, general mathematics journal publishing peer-reviewed papers of international standard across the whole spectrum of mathematics, but with the emphasis on applied analysis and differential equations.
An international journal, publishing six issues per year, Proceedings A has been publishing the highest-quality mathematical research since 1884. Recent issues have included a wealth of key contributors and considered research papers.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


