Unit fractions with shifted prime denominators

Abstract

We prove that any positive rational number is the sum of distinct unit fractions with denominators in $\{p-1 : p\textrm { prime}\}$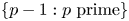. The same conclusion holds for the set $\{p-h : p\textrm { prime}\}$ 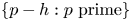for any $h\in \mathbb {Z}\backslash \{0\}$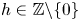, provided a necessary congruence condition is satisfied. We also prove that this is true for any subset of the primes of relative positive density, provided a necessary congruence condition is satisfied.