Threshold Graphs with an Arbitrary Large Gap Set

IF 16.4 1区化学 Q1 CHEMISTRY, MULTIDISCIPLINARY

Accounts of Chemical Research Pub Date : 2024-04-08 DOI:10.1007/s40840-024-01680-w

Abdullah Alazemi, Milica Anđelić, Haneen Zaidan

引用次数: 0

Abstract

An interval in which a given graph has no eigenvalues is called a gap interval. We show that for any real number R greater than \(\frac{1}{2}(-1+\sqrt{2})\), there exist infinitely many threshold graphs with gap interval (0, R). We provide a new recurrence relation for computing the characteristic polynomial of the threshold graphs and based on it, we conclude that the sequence of the least positive (resp. largest negative) eigenvalues of a certain sequence of threshold graphs is convergent. In some particular cases, we compute the limit points.

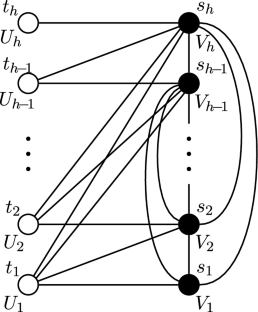
Abstract Image

查看原文本刊更多论文

具有任意大间隙集的阈值图

一个给定图形没有特征值的区间被称为间隙区间。我们证明，对于大于 \(\frac{1}{2}(-1+\sqrt{2})\)的任意实数 R，存在无限多个间隙区间为（0，R）的阈值图。我们为计算阈值图的特征多项式提供了一种新的递推关系，并基于这种关系得出结论：某个阈值图序列的最小正（或最大负）特征值序列是收敛的。在某些特殊情况下，我们会计算极限点。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Accounts of Chemical Research 化学-化学综合

CiteScore

31.40

自引率

1.10%

发文量

312

审稿时长

2 months

期刊介绍： Accounts of Chemical Research presents short, concise and critical articles offering easy-to-read overviews of basic research and applications in all areas of chemistry and biochemistry. These short reviews focus on research from the author’s own laboratory and are designed to teach the reader about a research project. In addition, Accounts of Chemical Research publishes commentaries that give an informed opinion on a current research problem. Special Issues online are devoted to a single topic of unusual activity and significance. Accounts of Chemical Research replaces the traditional article abstract with an article "Conspectus." These entries synopsize the research affording the reader a closer look at the content and significance of an article. Through this provision of a more detailed description of the article contents, the Conspectus enhances the article's discoverability by search engines and the exposure for the research.