Planar Graphs with the Maximum Number of Induced 4-Cycles or 5-Cycles

Abstract

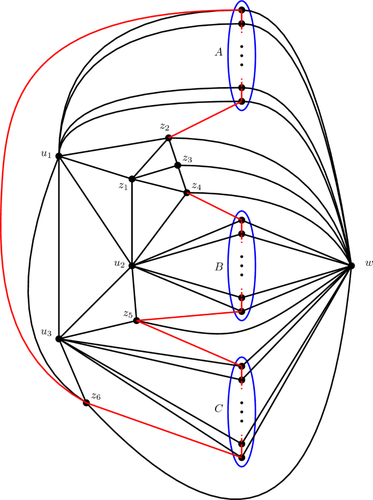
For large n we determine exactly the maximum numbers of induced \(C_4\) and \(C_5\) subgraphs that a planar graph on n vertices can contain. We show that \(K_{2,n-2}\) uniquely achieves this maximum in the \(C_4\) case, and we identify the graphs which achieve the maximum in the \(C_5\) case. This extends work in a paper by Hakimi and Schmeichel and a paper by Ghosh, Győri, Janzer, Paulos, Salia, and Zamora which together determine both maxima asymptotically.