Positive Einstein metrics with as the principal orbit
IF 1.4
1区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
We prove that there exists at least one positive Einstein metric on 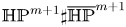 $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ for
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ for 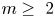 $m\geq ~2$. Based on the existence of the first Einstein metric, we give a criterion to check the existence of a second Einstein metric on
$m\geq ~2$. Based on the existence of the first Einstein metric, we give a criterion to check the existence of a second Einstein metric on  $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$. We also investigate the existence of cohomogeneity-one positive Einstein metrics on
$\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$. We also investigate the existence of cohomogeneity-one positive Einstein metrics on  $\mathbb {S}^{4m+4}$ and prove the existence of a non-standard Einstein metric on
$\mathbb {S}^{4m+4}$ and prove the existence of a non-standard Einstein metric on 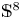 $\mathbb {S}^8$.
$\mathbb {S}^8$.
作为主轨道的正爱因斯坦度量
我们证明在 $mgeq ~2$ 的 $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ 上至少存在一个正的爱因斯坦度量。基于第一个爱因斯坦度量的存在,我们给出了一个标准来检验 $\mathbb {HP}^{m+1}\sharp \overline {\mathbb {HP}}^{m+1}$ 上第二个爱因斯坦度量的存在性。我们还研究了 $\mathbb {S}^{4m+4}$ 上同调一正的爱因斯坦度量的存在,并证明了 $\mathbb {S}^8$ 上非标准爱因斯坦度量的存在。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Compositio Mathematica
数学-数学
CiteScore
2.10
自引率
0.00%
发文量
62
审稿时长
6-12 weeks
期刊介绍:
Compositio Mathematica is a prestigious, well-established journal publishing first-class research papers that traditionally focus on the mainstream of pure mathematics. Compositio Mathematica has a broad scope which includes the fields of algebra, number theory, topology, algebraic and differential geometry and global analysis. Papers on other topics are welcome if they are of broad interest. All contributions are required to meet high standards of quality and originality. The Journal has an international editorial board reflected in the journal content.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


