On Alan Schoen’s I-WP minimal surface

IF 0.6 3区数学 Q3 MATHEMATICS

Annals of Global Analysis and Geometry Pub Date : 2024-03-27 DOI:10.1007/s10455-024-09951-2

Dami Lee, Matthias Weber, A. Tom Yerger

引用次数: 0

Abstract

We discuss in detail Alan Schoen’s I-WP surface, an embedded triply periodic minimal surface of genus 4 with cubical symmetries. We exhibit various geometric realizations of this surface with the same conformal structure and use them to prove that the associate family of the I-WP surface contains six surfaces congruent to I-WP at Bonnet angles that are multiples of \(60^\circ \).

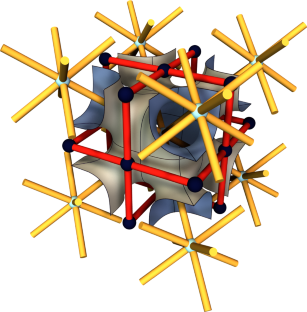
Abstract Image

查看原文本刊更多论文

关于艾伦-舍恩的 I-WP 最小曲面

我们详细讨论了艾伦-舍恩的 I-WP 曲面，这是一个内嵌的三周期极小曲面，属 4，具有立方对称性。我们展示了这个具有相同保角结构的曲面的各种几何实现，并用它们证明了 I-WP 曲面的关联族包含了六个与 I-WP 在波奈角为 \(60^\circ \) 的倍数时全等的、与 I-WP 在波奈角为 \(60^\circ \) 的倍数时全等的、与 I-WP 在波奈角为 \(60^\circ \) 的倍数时全等的曲面。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Annals of Global Analysis and Geometry 数学-数学

CiteScore

1.20

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： This journal examines global problems of geometry and analysis as well as the interactions between these fields and their application to problems of theoretical physics. It contributes to an enlargement of the international exchange of research results in the field. The areas covered in Annals of Global Analysis and Geometry include: global analysis, differential geometry, complex manifolds and related results from complex analysis and algebraic geometry, Lie groups, Lie transformation groups and harmonic analysis, variational calculus, applications of differential geometry and global analysis to problems of theoretical physics.