Direct and inverse problems of fractional Sturm–Liouville equation

IF 2 3区工程技术 Q2 ENGINEERING, MULTIDISCIPLINARY

Optimization and Engineering Pub Date : 2024-03-25 DOI:10.1007/s11081-024-09881-9

Zahra Kavousi Kalashmi, Hanif Mirzaei, Kazem Ghanbari

引用次数: 0

Abstract

In this paper we define a fractional Sturm–Liouville problem (FSLP) on [0, 1] subject to dirichlet boundary condition. First we discretize FSLP to obtain the corresponding matrix eigenvalue problem (MEP) of finite order N. In direct problem we give an efficient numerical algorithm to make good approximations for eigenvalues of FSLP by adding a correction term to eigenvalues of MEP. For inverse problem, using the idea of correction technique, we propose an algorithm for recovering the symmetric potential function using one given spectrum. Finally, we give some numerical examples to show the efficiency of the proposed algorithm.

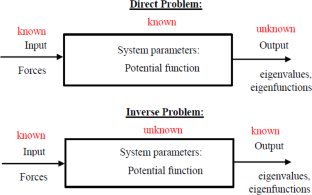
Abstract Image

查看原文本刊更多论文

分数 Sturm-Liouville 方程的直接和逆问题

本文定义了[0, 1]上的分数 Sturm-Liouville 问题 (FSLP)，该问题受 dirichlet 边界条件限制。首先，我们对 FSLP 进行离散化，得到相应的有限阶 N 矩阵特征值问题（MEP）。在直接问题中，我们给出了一种高效的数值算法，通过在 MEP 的特征值上添加修正项，对 FSLP 的特征值进行良好的近似。对于逆问题，我们利用修正技术的思想，提出了一种使用一个给定频谱恢复对称势函数的算法。最后，我们给出了一些数值示例来说明所提算法的效率。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Optimization and Engineering 工程技术-工程：综合

CiteScore

4.80

自引率

14.30%

发文量

审稿时长

>12 weeks

期刊介绍： Optimization and Engineering is a multidisciplinary journal; its primary goal is to promote the application of optimization methods in the general area of engineering sciences. We expect submissions to OPTE not only to make a significant optimization contribution but also to impact a specific engineering application. Topics of Interest: -Optimization: All methods and algorithms of mathematical optimization, including blackbox and derivative-free optimization, continuous optimization, discrete optimization, global optimization, linear and conic optimization, multiobjective optimization, PDE-constrained optimization & control, and stochastic optimization. Numerical and implementation issues, optimization software, benchmarking, and case studies. -Engineering Sciences: Aerospace engineering, biomedical engineering, chemical & process engineering, civil, environmental, & architectural engineering, electrical engineering, financial engineering, geosciences, healthcare engineering, industrial & systems engineering, mechanical engineering & MDO, and robotics.