Gevrey Class for Locally Three-Phase-Lag Thermoelastic Beam System

IF 1.6 2区数学 Q2 MATHEMATICS, APPLIED

Applied Mathematics and Optimization Pub Date : 2024-03-25 DOI:10.1007/s00245-024-10125-6

Jaime Muñoz Rivera, Elena Ochoa Ochoa, Ramón Quintanilla

引用次数: 0

Abstract

In this article we study the behavior of the solutions for the three-phase-lag heat equation with localized dissipation on an Euler–Bernoulli beam model. We show that semigroup S(t) associated with the problem is of Gevrey class 5 for \(t>0\). If the coefficients satisfy \(\tau _\alpha > k^{*}\tau _q\), the solutions are always exponentially stable.

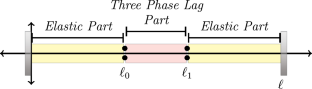
Abstract Image

查看原文本刊更多论文

局部三相滞后热弹性梁系统的 Gevrey 类

摘要本文研究了带有局部耗散的三相滞后热方程在欧拉-伯努利梁模型上的解的行为。我们证明与该问题相关的半群 S(t) 对于 \(t>0\) 是 Gevrey class 5 的。如果系数满足 \(\tau _\alpha > k^{*}\tau _q\) ，解总是指数稳定的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Applied Mathematics and Optimization 数学-应用数学

CiteScore

3.30

自引率

5.60%

发文量

103

审稿时长

>12 weeks

期刊介绍： The Applied Mathematics and Optimization Journal covers a broad range of mathematical methods in particular those that bridge with optimization and have some connection with applications. Core topics include calculus of variations, partial differential equations, stochastic control, optimization of deterministic or stochastic systems in discrete or continuous time, homogenization, control theory, mean field games, dynamic games and optimal transport. Algorithmic, data analytic, machine learning and numerical methods which support the modeling and analysis of optimization problems are encouraged. Of great interest are papers which show some novel idea in either the theory or model which include some connection with potential applications in science and engineering.