A Note on Internal Partitions: The 5-Regular Case and Beyond
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
An internal or friendly partition of a graph is a partition of the vertex set into two nonempty sets so that every vertex has at least as many neighbours in its own class as in the other one. It has been shown that apart from finitely many counterexamples, every 3, 4 or 6-regular graph has an internal partition. In this note we focus on the 5-regular case and show that among the subgraphs of minimum degree at least 3 of 5-regular graphs, there are some which have small intersection. We also discuss the existence of internal partitions in some families of Cayley graphs, notably we determine all 5-regular Abelian Cayley graphs which do not have an internal partition.
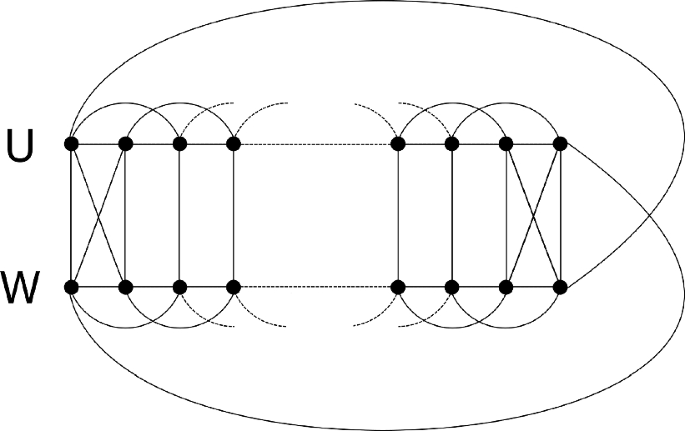
关于内部分区的说明:5-常规案例及其他
图的内部分割或友好分割是指将顶点集分割成两个非空集,使每个顶点在自己的类中至少有和在另一个类中一样多的邻居。研究表明,除了有限多个反例之外,每个 3、4 或 6 规则图都有一个内部分割。在本论文中,我们将重点讨论 5 不规则图,并证明在 5 不规则图的最小度至少为 3 的子图中,有一些具有小交集。我们还讨论了某些 Cayley 图族中内部分区的存在,特别是我们确定了所有不存在内部分区的 5 不规则阿贝尔 Cayley 图。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Graphs and Combinatorics
数学-数学
CiteScore
1.00
自引率
14.30%
发文量
160
审稿时长
6 months
期刊介绍:
Graphs and Combinatorics is an international journal devoted to research concerning all aspects of combinatorial mathematics. In addition to original research papers, the journal also features survey articles from authors invited by the editorial board.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


