Sum of series and new relations for Mittag-Leffler functions

IF 2.5 2区数学 Q1 MATHEMATICS

Fractional Calculus and Applied Analysis Pub Date : 2024-03-19 DOI:10.1007/s13540-024-00266-4

Sarah A. Deif, E. Capelas de Oliveira

引用次数: 0

Abstract

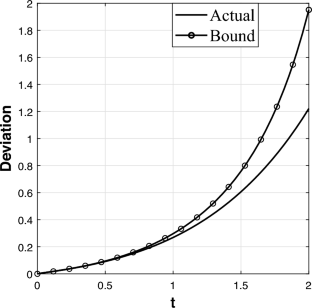
An integral equation is constructed relating the three-parameter Mittag-Leffler function with a perturbed one, from which a new property is derived. The latter helps in finding new sums of series of Mittag-Leffler functions. Also, a bound is obtained for the Mittag-Leffler function, allowing to perform a sensitivity analysis, being vital in the solution of fractional differential equations. The bound is also tested on a numerical example.

Abstract Image

查看原文本刊更多论文

Mittag-Leffler 函数的级数之和与新关系式

构建了一个三参数米塔格-勒弗勒函数与扰动函数之间的积分方程，并从中得出了一个新的性质。后者有助于找到新的米塔格-勒弗勒函数数列和。此外，还获得了 Mittag-Leffler 函数的约束，从而可以进行敏感性分析，这对分数微分方程的求解至关重要。该约束还在一个数值示例中进行了检验。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Fractional Calculus and Applied Analysis MATHEMATICS, APPLIED-MATHEMATICS, INTERDISCIPLINARY APPLICATIONS

CiteScore

4.70

自引率

16.70%

发文量

101

期刊介绍： Fractional Calculus and Applied Analysis (FCAA, abbreviated in the World databases as Fract. Calc. Appl. Anal. or FRACT CALC APPL ANAL) is a specialized international journal for theory and applications of an important branch of Mathematical Analysis (Calculus) where differentiations and integrations can be of arbitrary non-integer order. The high standards of its contents are guaranteed by the prominent members of Editorial Board and the expertise of invited external reviewers, and proven by the recently achieved high values of impact factor (JIF) and impact rang (SJR), launching the journal to top places of the ranking lists of Thomson Reuters and Scopus.