Diverse Pairs of Matchings

IF 0.9 4区计算机科学 Q4 COMPUTER SCIENCE, SOFTWARE ENGINEERING

Algorithmica Pub Date : 2024-03-15 DOI:10.1007/s00453-024-01214-7

Fedor V. Fomin, Petr A. Golovach, Lars Jaffke, Geevarghese Philip, Danil Sagunov

引用次数: 0

Abstract

We initiate the study of the Diverse Pair of (Maximum/ Perfect) Matchings problems which given a graph G and an integer k, ask whether G has two (maximum/perfect) matchings whose symmetric difference is at least k. Diverse Pair of Matchings (asking for two not necessarily maximum or perfect matchings) is \(\textsf{NP}\)-complete on general graphs if k is part of the input, and we consider two restricted variants. First, we show that on bipartite graphs, the problem is polynomial-time solvable, and second we show that Diverse Pair of Maximum Matchings is \(\textsf{FPT}\) parameterized by k. We round off the work by showing that Diverse Pair of Matchings has a kernel on \({\mathcal {O}}(k^2)\) vertices.

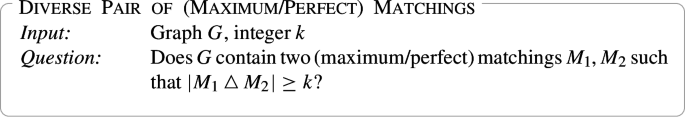
Abstract Image

查看原文本刊更多论文

多样化的配对

我们开始研究"（最大/完美）匹配的多样性对"（Diverse Pair of (Maximum/ Perfect) Matchings）问题，给定一个图 G 和一个整数 k，问 G 是否有两个对称差至少为 k 的（最大/完美）匹配。首先，我们证明了在二叉图上，这个问题是多项式时间可解的；其次，我们证明了以 k 为参数的 Diverse Pair of Maximum Matchings 是 \(\textsf{FPT}\)的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Algorithmica 工程技术-计算机：软件工程

CiteScore

2.80

自引率

9.10%

发文量

158

审稿时长

12 months

期刊介绍： Algorithmica is an international journal which publishes theoretical papers on algorithms that address problems arising in practical areas, and experimental papers of general appeal for practical importance or techniques. The development of algorithms is an integral part of computer science. The increasing complexity and scope of computer applications makes the design of efficient algorithms essential. Algorithmica covers algorithms in applied areas such as: VLSI, distributed computing, parallel processing, automated design, robotics, graphics, data base design, software tools, as well as algorithms in fundamental areas such as sorting, searching, data structures, computational geometry, and linear programming. In addition, the journal features two special sections: Application Experience, presenting findings obtained from applications of theoretical results to practical situations, and Problems, offering short papers presenting problems on selected topics of computer science.