Global index of real polynomials
IF 0.9
3区 数学
Q1 MATHEMATICS
Proceedings of the Royal Society of Edinburgh Section A-Mathematics
Pub Date : 2024-03-18
DOI:10.1017/prm.2024.23
引用次数: 0
Abstract
We develop two methods for expressing the global index of the gradient of a 2 variable polynomial function $f$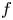 : in terms of the atypical fibres of $f$
: in terms of the atypical fibres of $f$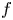 , and in terms of the clusters of Milnor arcs at infinity. These allow us to derive upper bounds for the global index, in particular refining the one that was found by Durfee in terms of the degree of $f$
, and in terms of the clusters of Milnor arcs at infinity. These allow us to derive upper bounds for the global index, in particular refining the one that was found by Durfee in terms of the degree of $f$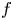 .
.
实多项式的全局指数
我们开发了两种方法来表达二变多项式函数 $f$ 梯度的全局指数:用 $f$ 的非典型纤维表示,以及用无穷远处的米尔诺弧群表示。通过这些方法,我们可以推导出全局指数的上限,特别是完善了杜菲根据 $f$ 的阶数所发现的上限。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.00
自引率
0.00%
发文量
72
审稿时长
6-12 weeks
期刊介绍:
A flagship publication of The Royal Society of Edinburgh, Proceedings A is a prestigious, general mathematics journal publishing peer-reviewed papers of international standard across the whole spectrum of mathematics, but with the emphasis on applied analysis and differential equations.
An international journal, publishing six issues per year, Proceedings A has been publishing the highest-quality mathematical research since 1884. Recent issues have included a wealth of key contributors and considered research papers.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


