Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations
IF 0.9
3区 数学
Q1 MATHEMATICS
Proceedings of the Royal Society of Edinburgh Section A-Mathematics
Pub Date : 2024-03-11
DOI:10.1017/prm.2024.26
引用次数: 0
Abstract
In this paper, we are concerned with the ground states of the following planar Kirchhoff-type problem:\[ -\left(1+b\displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u+\omega u=|u|^{p-2}u, \quad x\in\mathbb{R}^2. \]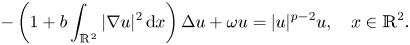 where $b,\, \omega >0$
where $b,\, \omega >0$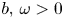 are constants, $p>2$
are constants, $p>2$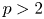 . Based on variational methods, regularity theory and Schwarz symmetrization, the equivalence of ground state solutions for the above problem with the minimizers for some minimization problems is obtained. In particular, a new scale technique, together with Lagrange multipliers, is delicately employed to overcome some intrinsic difficulties.
. Based on variational methods, regularity theory and Schwarz symmetrization, the equivalence of ground state solutions for the above problem with the minimizers for some minimization problems is obtained. In particular, a new scale technique, together with Lagrange multipliers, is delicately employed to overcome some intrinsic difficulties.
平面基尔霍夫型方程基态解的必要条件和充分条件
在本文中,我们关注以下平面基尔霍夫型问题的基态:\[ -\left(1+b\displaystyle\int_{\mathbb{R}^2}|\nabla u|^2\,{\rm d}x\right)\Delta u+\omega u=|u|^{p-2}u, \quad x\in\mathbb{R}^2.\其中$b,\,\omega >0$为常数,$p>2$。基于变分法、正则性理论和施瓦茨对称性,得到了上述问题的基态解与某些最小化问题的最小值的等价性。特别是采用了一种新的尺度技术和拉格朗日乘法器,巧妙地克服了一些内在困难。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.00
自引率
0.00%
发文量
72
审稿时长
6-12 weeks
期刊介绍:
A flagship publication of The Royal Society of Edinburgh, Proceedings A is a prestigious, general mathematics journal publishing peer-reviewed papers of international standard across the whole spectrum of mathematics, but with the emphasis on applied analysis and differential equations.
An international journal, publishing six issues per year, Proceedings A has been publishing the highest-quality mathematical research since 1884. Recent issues have included a wealth of key contributors and considered research papers.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


