Every finite graph arises as the singular set of a compact 3-D calibrated area minimizing surface
IF 2.7
1区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
Given any (not necessarily connected) combinatorial finite graph and any compact smooth 6-manifold with the third Betti number , we construct a calibrated 3-dimensional homologically area minimizing surface on equipped in a smooth metric , so that the singular set of the surface is precisely an embedding of this finite graph. Moreover, the calibration form near the singular set is a smoothly twisted special Lagrangian form. The constructions are based on some unpublished ideas of Professor Camillo De Lellis and Professor Robert Bryant.
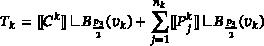
每个有限图形都是一个紧凑的三维校准面积最小曲面的奇异集
给定任意(不一定相连的)组合有限图和任意具有第三个贝蒂数的紧凑光滑 6-manifold,我们在光滑度量中在配备上构造了一个校准的三维同源面积最小曲面,因此曲面的奇点集正是这个有限图的嵌入。此外,奇点集附近的校准形式是一种平滑扭曲的特殊拉格朗日形式。这些构造基于卡米洛-德莱利斯教授和罗伯特-布莱恩特教授一些未发表的观点。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
6.70
自引率
3.30%
发文量
59
审稿时长
>12 weeks
期刊介绍:
Communications on Pure and Applied Mathematics (ISSN 0010-3640) is published monthly, one volume per year, by John Wiley & Sons, Inc. © 2019.
The journal primarily publishes papers originating at or solicited by the Courant Institute of Mathematical Sciences. It features recent developments in applied mathematics, mathematical physics, and mathematical analysis. The topics include partial differential equations, computer science, and applied mathematics. CPAM is devoted to mathematical contributions to the sciences; both theoretical and applied papers, of original or expository type, are included.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


