An embedding theorem for subshifts over amenable groups with the comparison property
IF 0.8
3区 数学
Q2 MATHEMATICS
引用次数: 0
Abstract
We obtain the following embedding theorem for symbolic dynamical systems. Let G be a countable amenable group with the comparison property. Let X be a strongly aperiodic subshift over G. Let Y be a strongly irreducible shift of finite type over G that has no global period, meaning that the shift action is faithful on Y. If the topological entropy of X is strictly less than that of Y and Y contains at least one factor of X, then X embeds into Y. This result partially extends the classical result of Krieger when  $G = \mathbb {Z}$ and the results of Lightwood when
$G = \mathbb {Z}$ and the results of Lightwood when 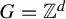 $G = \mathbb {Z}^d$ for
$G = \mathbb {Z}^d$ for 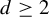 $d \geq 2$. The proof relies on recent developments in the theory of tilings and quasi-tilings of amenable groups.
$d \geq 2$. The proof relies on recent developments in the theory of tilings and quasi-tilings of amenable groups.
具有比较性质的可调和群上子移的嵌入定理
我们得到以下符号动力系统的嵌入定理。设 G 是具有比较性质的可数可调群。让 X 是 G 上的强无周期子移位。让 Y 是 G 上有限类型的强不可还原移位,它没有全局周期,即移位作用在 Y 上是忠实的。如果 X 的拓扑熵严格小于 Y 的拓扑熵,且 Y 至少包含 X 的一个因子,那么 X 嵌入 Y。这个结果部分地扩展了克里格在 $G = \mathbb {Z}$ 时的经典结果,以及莱特伍德在 $G = \mathbb {Z}^d$ 时对于 $d \geq 2$ 的结果。证明依赖于可平分群的倾斜和准倾斜理论的最新发展。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.70
自引率
11.10%
发文量
113
审稿时长
6-12 weeks
期刊介绍:
Ergodic Theory and Dynamical Systems focuses on a rich variety of research areas which, although diverse, employ as common themes global dynamical methods. The journal provides a focus for this important and flourishing area of mathematics and brings together many major contributions in the field. The journal acts as a forum for central problems of dynamical systems and of interactions of dynamical systems with areas such as differential geometry, number theory, operator algebras, celestial and statistical mechanics, and biology.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


