Tracial weights on topological graph algebras
IF 0.8
3区 数学
Q2 MATHEMATICS
引用次数: 0
Abstract
We describe two kinds of regular invariant measures on the boundary path space 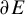 $\partial E$ of a second countable topological graph E, which allows us to describe all extremal tracial weights on
$\partial E$ of a second countable topological graph E, which allows us to describe all extremal tracial weights on 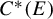 $C^{*}(E)$ which are not gauge-invariant. Using this description, we prove that all tracial weights on the C
$C^{*}(E)$ which are not gauge-invariant. Using this description, we prove that all tracial weights on the C $^{*}$-algebra
$^{*}$-algebra 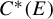 $C^{*}(E)$ of a second countable topological graph E are gauge-invariant when E is free. This in particular implies that all tracial weights on
$C^{*}(E)$ of a second countable topological graph E are gauge-invariant when E is free. This in particular implies that all tracial weights on 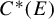 $C^{*}(E)$ are gauge-invariant when
$C^{*}(E)$ are gauge-invariant when 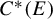 $C^{*}(E)$ is simple and separable.
$C^{*}(E)$ is simple and separable.
拓扑图代数上的三角形权重
我们描述了第二可数拓扑图 E 的边界路径空间 $\partial E$ 上的两种正则不变度量,这使我们能够描述 $C^{*}(E)$ 上所有不是轨距不变的极值三边权重。利用这一描述,我们证明了当第二个可数拓扑图 E 的 C$^{*}$ 代数 $C^{*}(E)$ 是自由的时候,其上的所有三项权重都是轨距不变的。这尤其意味着,当$C^{*}(E)$是简单可分的时候,$C^{*}(E)$上的所有三项权重都是规整不变的。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.70
自引率
11.10%
发文量
113
审稿时长
6-12 weeks
期刊介绍:
Ergodic Theory and Dynamical Systems focuses on a rich variety of research areas which, although diverse, employ as common themes global dynamical methods. The journal provides a focus for this important and flourishing area of mathematics and brings together many major contributions in the field. The journal acts as a forum for central problems of dynamical systems and of interactions of dynamical systems with areas such as differential geometry, number theory, operator algebras, celestial and statistical mechanics, and biology.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


