IDEMPOTENT GENERATORS OF INCIDENCE ALGEBRAS

IF 0.6 4区数学 Q3 MATHEMATICS

Bulletin of the Australian Mathematical Society Pub Date : 2024-03-05 DOI:10.1017/s0004972724000078

N. A. KOLEGOV

引用次数: 0

Abstract

The minimum number of idempotent generators is calculated for an incidence algebra of a finite poset over a commutative ring. This quantity equals either 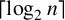Abstract Image $\lceil \log _2 n\rceil $ or 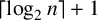$\lceil \log _2 n\rceil +1$, where n is the cardinality of the poset. The two cases are separated in terms of the embedding of the Hasse diagram of the poset into the complement of the hypercube graph.

查看原文本刊更多论文

幂等生成数

计算了交换环上有限正集的入射代数的最小幂生子数。这个数量要么等于 $\lceil \log _2 n\rceil $，要么等于 $\lceil \log _2 n\rceil +1 $，其中 n 是正集的万有引力。这两种情况可以通过将正集的哈塞图嵌入超立方图的补集来区分。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Bulletin of the Australian Mathematical Society 数学-数学

CiteScore

1.20

自引率

14.30%

发文量

149

审稿时长

4-8 weeks

期刊介绍： Bulletin of the Australian Mathematical Society aims at quick publication of original research in all branches of mathematics. Papers are accepted only after peer review but editorial decisions on acceptance or otherwise are taken quickly, normally within a month of receipt of the paper. The Bulletin concentrates on presenting new and interesting results in a clear and attractive way. Published Bi-monthly Published for the Australian Mathematical Society