Diameter estimates for surfaces in conformally flat spaces
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
The aim of this paper is to give an upper bound for the intrinsic diameter of a surface with boundary immersed in a conformally flat three dimensional Riemannian manifold in terms of the integral of the mean curvature and of the length of its boundary. Of particular interest is the application of the inequality to minimal surfaces in the three-sphere and in the hyperbolic space. Here the result implies an a priori estimate for connected solutions of Plateau’s problem, as well as a necessary condition on the boundary data for the existence of such solutions. The proof follows a construction of Miura and uses a diameter bound for closed surfaces obtained by Topping and Wu–Zheng.
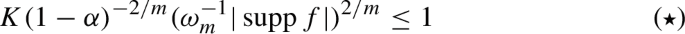
共形平面空间中曲面的直径估计值
本文旨在根据平均曲率积分和边界长度积分,给出浸没在保角平坦三维黎曼流形中的有边界曲面的本征直径上限。特别令人感兴趣的是将不等式应用于三球面和双曲空间中的最小曲面。在这里,该结果意味着对普拉托问题的连通解的先验估计,以及这种解存在的边界数据的必要条件。证明沿用了三浦的构造,并使用了托平与吴征获得的封闭曲面的直径约束。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Manuscripta Mathematica
数学-数学
CiteScore
1.40
自引率
0.00%
发文量
86
审稿时长
6-12 weeks
期刊介绍:
manuscripta mathematica was founded in 1969 to provide a forum for the rapid communication of advances in mathematical research. Edited by an international board whose members represent a wide spectrum of research interests, manuscripta mathematica is now recognized as a leading source of information on the latest mathematical results.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


