A Construction of Pseudo-reductive Groups with Non-reduced Root Systems
IF 0.4
3区 数学
Q4 MATHEMATICS
引用次数: 0
Abstract
We describe a straightforward construction of the pseudo-split absolutely pseudo-simple groups of minimal type with irreducible root systems of type \(BC_n\); these exist only in characteristic 2. We also give a formula for the dimensions of their irreducible modules.
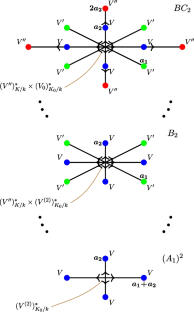
构建具有非还原根系统的伪还原群
我们描述了具有 \(BC_n\) 型不可还原根系统的极小型伪分裂绝对伪简单群的直接构造;这些群只存在于特征 2 中。我们还给出了它们的不可还原模块的维数公式。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Transformation Groups
数学-数学
CiteScore
1.60
自引率
0.00%
发文量
100
审稿时长
9 months
期刊介绍:
Transformation Groups will only accept research articles containing new results, complete Proofs, and an abstract. Topics include: Lie groups and Lie algebras; Lie transformation groups and holomorphic transformation groups; Algebraic groups; Invariant theory; Geometry and topology of homogeneous spaces; Discrete subgroups of Lie groups; Quantum groups and enveloping algebras; Group aspects of conformal field theory; Kac-Moody groups and algebras; Lie supergroups and superalgebras.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


